第 2 章 古老的秘密在现代机器上延续(Ancient secret keeping on modern machines)
本章内容包括:
- 如何建立一个基础的 Haskell 项目并运行代码
- Haskell 常见数据类型与函数的工作原理
- 使用字符串和列表执行基本操作
- 通过守卫(guards)与模式匹配(pattern matching)处理不同情况
- 操作不可变数据并表示数据转换
在上一章中,我们了解了 Haskell 是什么,并讨论了它在语言设计上的一些独特之处。我们还学习了纯函数(pure functions)的特性,以及像 Haskell 这样的纯函数式语言是如何组织程序结构的。 这些概念固然重要,但光说不练是没有意义的——理论必须结合实践才能真正掌握。现在,是时候动手实现我们的第一个项目了!
学习任何一门编程语言,总得从某处开始。虽然我可以用数学推导或学术练习来“折磨”你,但这本书的主题更轻松一点。有人甚至会说这些内容挺有趣——不过你不一定得这么认为。本章主要介绍 Haskell 的语法以及编写程序的基本方式。由于 Haskell 的核心理念与其他主流语言大相径庭,你最好暂时“忘掉”自己熟悉的一些编程模式。可变变量?静态数据?命令式控制流?——这些概念在我们即将踏入的世界中都是不存在的“黑魔法”。
我知道刚才的比喻有点夸张,所以让我解释一下:Haskell 的纯函数式设计一开始可能会让人望而生畏。如果你之前没有接触过函数式语言,那么本章的概念可能会显得有些奇怪。这主要是因为这种语言的设计思路与我们熟悉的命令式语言截然不同。举个例子,Haskell 没有循环! 当然,Haskell 有很多方式可以实现与循环类似的功能。严格来说,我们根本不需要循环——但这也意味着我们必须重新思考许多关于“编程”的旧习惯。
虽然这听起来有些可怕,但这趟旅程非常值得。Haskell 的核心概念是普适的——几乎可以在任何其他语言中实现。学习纯函数式编程的过程,其实是在学习一种全新的思维方式:如何用数学化的思考方式写出正确且可靠的程序。
本章将从建立一个新的 Haskell 项目开始,并使用 Haskell 编译器的交互模式(REPL)来编写与测试原型代码。接着,我们会介绍 Haskell 的多种基本数据类型,以及如何为函数和表达式定义类型。然后我们将学习如何编写函数、操作字符串与列表;进一步,通过守卫和模式匹配深入理解函数的结构与控制逻辑。最后,本章会介绍并使用内置的 map 函数。
2.1 Haskell 入门(A primer on Haskell)
现代计算机系统几乎都依赖外部网络才能高效工作。无论是通过 NTP 或 PTP 进行时间同步、在分布式 NoSQL 数据库中存储数据,还是晚上看一段 4K 猫咪视频——网络无处不在。但这也带来了一个重大问题:**我们必须保护在公共网络中传输的个人数据。**我们不能把自己的银行账户信息对着森林大喊一遍,然后祈祷没人听见。
正如你可能已经猜到的,解决方案就是——加密(encryption) 。加密的基本思路是使用一个双方共享的“密钥”来对信息进行编码。如今,密码学(cryptography)已深深融入我们的日常生活,而它的研究领域也在不断发展,提出越来越复杂的算法与协议来实现“安全保密”的目标。
在本章中,我们将实现一种最古老、最简单的加密方法——凯撒密码(Caesar’s cipher)。它在现实世界中早已不再安全,但它能很好地帮助我们理解函数式编程的基本原理。
2.1.1 凯撒密码(Caesar’s cipher)
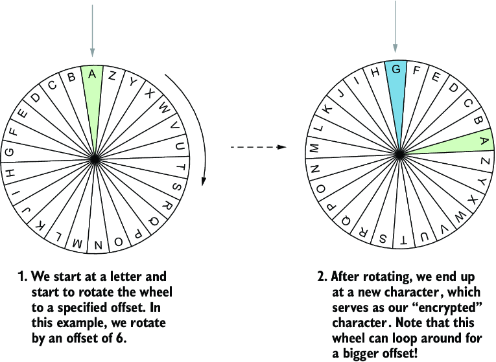
这个古老的算法是如何工作的呢?凯撒密码通过将字母表中的每个字母按固定偏移量替换成另一个字母来实现加密。也就是说,你可以根据字母在字母表中的位置选择一个新的字母,从而加密原始字母。
你可以把字母表想象成一个轮盘,所有字母按顺序排列成一个圆圈。从某个字母开始,将轮盘旋转一定偏移量,就会得到新的字母。这个概念在图 2.1 中有示意。
图 2.1 字母替换轮盘
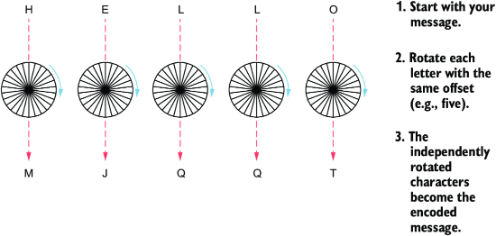
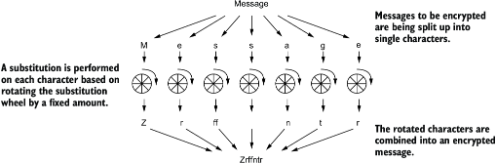
通过对信息中的每个字母进行变换,我们就可以对整条信息加密!用于这种变换的偏移量就是算法的加密密钥,需要通信双方都知道。在解密时,只需反向执行同样的操作,就可以恢复原始信息。图 2.2 展示了一个例子:一个小信息被加密时使用了偏移量 5。
图 2.2 凯撒密码加密示例
如果只加密基本拉丁字母(并且大写字母和小写字母各自使用自己的字母表),会出现一种有趣的对称性:当偏移量为 13 时,加密和解密互相抵消,也就是说可以用完全相同的方法进行加密和解密。这种特殊的凯撒密码称为 ROT13,通常用作文字混淆工具,因为实现非常简单。一些编辑器,如 Vim 和 Emacs,甚至内置了 ROT13 功能!
示例:Vfa’g gung arng?
⚠️ 警告 为了保护你和他人的数据安全,切勿在任何应用程序中使用这种加密方法!
2.1.2 新建项目(A new project)
我们先用 stack 创建一个新项目。如果你还没有安装 stack,请参考附录 A。工具链安装好后,可以在操作系统中打开命令行。在 macOS 上可以使用 iTerm,Windows 上可能是 cmd,而 Linux 上选择更多样。
然后,进入你希望存放项目的工作目录,并运行以下命令:
stack new caesar
这会创建一个名为 caesar 的新目录,其中已经包含了 Haskell 项目的预设结构。
让我们看看 stack 创建的目录结构(见清单 2.1):
- 它包含一些元信息文件,如
CHANGELOG.md、LICENSE和README.md,用于记录变更、授权信息和项目使用说明(如果项目发布的话)。 caesar.cabal、package.yaml和stack.yaml对配置依赖和编译选项很重要,但在本项目中我们暂时不修改它们。
项目的核心目录是 app 和 src:
app目录包含程序的入口模块(main),即编译后的可执行文件的起点,就像 C 或 Java 中的main函数。src目录包含库代码,包括所有模块、类型和函数定义,可以作为独立库使用。这样,我们可以在多个可执行文件中复用相同功能,或者将项目编译为库而非可执行文件。test目录可以用来存放测试套件,用于测试库和可执行文件的代码(将在第 9 章详细讲解)。
清单 2.1 新建 stack 项目的目录结构
caesar
├── CHANGELOG.md
├── LICENSE
├── README.md
├── Setup.hs
├── app #1
│ └── Main.hs
├── caesar.cabal
├── package.yaml
├── src #2
│ └── Lib.hs
├── stack.yaml
└── test #3
└── Spec.hs
#1 用于构建可执行文件的模块
#2 用于构建独立库的模块
#3 用于测试库代码的测试套件
目前我们唯一需要关注的文件是 Lib.hs,将在其中编写函数,并在 Haskell 编译器的交互模式中使用。
接下来,我们尝试 REPL(Read–Eval–Print Loop) 来熟悉 Haskell 的语法。运行:
stack repl
这会启动 GHCi(Glasgow Haskell Compiler 的交互模式),提示符如下:
ghci>
如果当前工作目录是通过 stack 创建的项目,模块和定义会自动加载到 GHCi 中,可以直接测试。
例如,我们尝试一些基本算术:
ghci> a = 1 :: Int
ghci> b = 2 :: Int
ghci> c = a + b
ghci> c
3
从上面的例子可以看到,我们可以在代码中定义变量,将值与名字关联。REPL 会对每条输入进行求值:赋值语句本身没有结果,而对变量求值则会显示它的值。Haskell 使用 :: 指明值的类型。
注意 在 GHCi 中输入像
1 + 1这样的表达式,会得到结果 2,但可能还会看到关于类型默认的警告。如果不希望看到这些警告,可以使用:set -Wno-type-defaults。
接下来我们用函数来实践函数式编程。Haskell 函数的语义与其他语言类似,基本语法很简单:
函数名 参数列表 = 函数定义
例如:
square x = x * x
定义了一个单参数函数 square,将参数自身相乘。函数调用如下:
square 2
Haskell 不像其他语言那样使用括号或逗号分隔参数。在 REPL 中输入 square 2 会求值并打印结果。
多行输入示例如下:
ghci> :{ #1
ghci| square :: Int -> Int
ghci| square x = x * x
ghci| :} #2
ghci> square 2
4
:{开始多行输入:}结束多行输入
为 square 指定类型不是必需的,但不写会出现警告。
REPL 适合快速原型和简单测试,但写大函数时可能不太方便。这就是为什么我们会把大部分实现放在 Lib.hs 中。
2.1.3 第一个模块(The first module)
Lib.hs 文件会有一个非常基础的结构,用于展示 Haskell 模块的基本组成。模块包含我们的代码,包括定义和实现,它们帮助我们组织项目,将相关代码分组。
通常模块名必须与文件路径一致(Main 模块除外,取决于项目配置)。在这个简单例子中,模块位于 src 目录的最高层,因此模块名就是文件名去掉后缀即可。此外,模块可以定义导出列表(export list),用来指定哪些定义可以被其他模块访问,因为模块也可以导入其他模块。这个文件可能长这样:
清单 2.2 stack 创建的简单模块示例
module Lib --1
( someFunc --2
) where
someFunc :: IO () --3
someFunc = putStrLn "someFunc" --4
--1定义模块名--2指定导出列表--3给出类型签名--4提供函数定义
这个模块本身没有实际用途,只是用来演示模块如何构建。我们看到一个名为 someFunc 的 IO 操作定义,它被模块名后的导出列表导出。IO 操作的具体内容将在第 3 章讲解,目前我们不需要关注。
导入其他模块最基本的方法是使用 import 语句。它会导入指定模块的所有导出定义(如果没有导出列表,则导入全部)。这种方式适合导入提供独特函数的工具模块,但有可能出现名字冲突。这时可以在函数名前加上模块名,如 ModuleName.x 来指定使用哪个定义。
接下来看看 Main.hs,了解如何导入 Lib 模块以及“主模块”的样子。主模块包含 main 操作,是程序的入口。我们暂时不关心 main 做什么,只需把它当作一个被调用的函数即可。
清单 2.3 stack 创建的简单 Main 模块
module Main where
import Lib --1
main :: IO () --2
main = someFunc
--1导入模块--2定义主操作
在本项目中,我们所有实现都在 Lib 模块,并用 GHCi 测试,因此可以暂时忽略 Main 模块。为了让可执行文件能编译通过,并避免 IDE 报错,我们可以把 Main.hs 改为只打印 Hello World,不再导入 Lib:
module Main where
main :: IO ()
main = putStrLn "Hello World"
回到 Lib.hs,进一步熟悉 Haskell。我们可以先删除导出列表和 someFunc,模块就变成:
module Lib where
干净整洁——一个全新的开始!我们可以在这个模块中定义函数,而不必在 GHCi 中逐行输入。
定义函数后,需要把它加入导出列表,这样其他模块才能访问:
module Lib
( square,
)
where
square :: Int -> Int
square x = x * x
保存文件后,就可以加载模块了。方法是进入项目目录,运行:
stack repl
注意 记得把希望被其他模块访问的函数和类型加入导出列表,否则模块外无法找到它们。虽然可以省略导出列表导出所有定义,但这被认为是不良编码风格,会导致代码难以管理。
模块会自动加载。之后,你就可以在新打开的 GHCi 中使用这些函数。请保持这个 GHCi 会话打开,因为我们将用它进行原型开发。
2.2 常见类型与奇妙函数(Typical types and fantastic functions)
为了让我们的项目结构更清晰,我们首先要思考要处理的数据类型。更确切地说,就是要考虑数据的类型(types)。在 Haskell 这样的语言中,类型至关重要。与一些其他语言类似,Haskell 是静态类型语言(statically typed)——类型在编译时就已经确定,运行时不能动态改变。也就是说,一旦变量拥有某种类型,在程序执行期间这个类型就不会变化。此外,Haskell 还使用类型推导(type inference)。如果没有显式地写出类型,Haskell 会尝试根据上下文自动推导类型。通常这种机制非常可靠,不过在某些情况下,我们需要显式地告诉 Haskell 某个表达式或变量的类型。正因为有类型推导机制,我们之前在 GHCi 中输入的那些函数定义,即使没写类型声明,也能正常工作。
然而,良好的编程风格是:在模块的顶层定义(top-level definitions)中,显式地写出类型声明。这可以通过类型表达式(type expression) 来实现。最基本的形式如下:
name :: type
它表示给某个名称(或称标识符)分配一个类型。名称只是值的一个映射,因此这实际上是在声明某个值应该具有什么类型。通常类型表达式会紧跟着具体的定义,尽管这不是强制要求。类型表达式是程序中语义表达式(semantic expressions)的一个有趣补充。我们已经见过语义表达式,例如 x * x。在求值时,这个表达式会产生一个值。如果一个语义表达式带有类型表达式,这意味着产生的值具有该类型表达式指定的类型,而不是“语义表达式本身”的类型。稍后在研究函数时,我们会更清楚地看到这种区别。
2.2.1 原子级别的类型(Types on the atomic level)
了解了类型表达式的基本语法后,我们再看看类型的实际样子。最简单的类型就是原子类型(atomic types),它们是程序中最常用的类型。表 2.1 列出了一些常见的原子类型。
| 名称 (Name) | 描述 (Description) | 示例 (Examples) |
|---|---|---|
| Bool | 布尔真值 | True, False |
| Char | Unicode 字符 | 'a', 'A', '1' |
| Integer | 任意精度整数 | -1, 9999999 |
| Int | 固定精度整数 | -1, 10 |
| Float | 单精度浮点数 | 3.1415, -1, 1e2 |
| Double | 双精度浮点数 | 1e-2, 9.99999 |
可以看到,一些数值类型的示例值看起来是相同的。当我们使用这些“模棱两可”的值时,Haskell 的类型推导机制就会介入,尝试推断正确的类型。
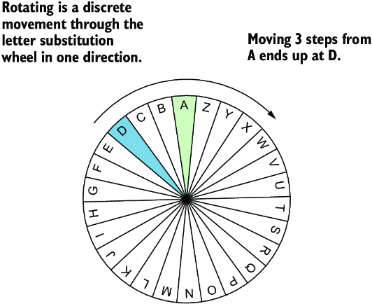
有了这些类型知识后,我们可以开始思考如何实现加密轮的旋转(见图 2.3)。每一次轮盘旋转都是从一个字母移动到下一个字母的离散步骤,因此加密密钥可以简单地表示为一个 Int。消息由字母组成,因此是若干 Char 值的集合。我们要编写的函数将主要处理这些类型。
图 2.3 字母替换轮
需要特别注意的一点是:**这些原子类型本身也是类型表达式!**这意味着我们可以给出一个属于该类型的值(或语义表达式),形式如下:
kilo :: Int
kilo = 1000
mega :: Int
mega = kilo ^ (2 :: Int)
nano :: Double
nano = 1e-9
在这里,我们定义了三个表示单位前缀的值。
- 我们将标识符
kilo声明为类型Int,这就明确指定了它是一个整数。 - 而
nano是一个类型为Double的浮点数。 mega的定义通过对kilo进行运算(即指数运算^)得到,因此它必须与kilo具有相同的类型。
这是因为数值运算符通常接受并返回相同类型的值。
2.2.2 列表与元组(Lists and tuples)
仅仅依靠简单的原子类型,还不足以构建有用的数据结构。在我们的例子中,我们需要某种方式来表示一组字母的集合。幸运的是,Haskell 提供了一些更复杂的类型,本节我们将详细介绍它们。
第一个要介绍的就是 列表。列表是 Haskell(以及许多其他函数式编程语言)的核心构建块之一。它的概念非常简单:列表是一个同质(homogeneous)的值序列,也就是说,列表中的所有元素必须具有相同的类型。我们可以通过用方括号包裹的逗号分隔值来定义列表。列表没有固定长度,可以动态增长。示例如下:
intList :: [Int]
intList = [1, 2, 3]
boolList :: [Bool]
boolList = [True]
floatList :: [Float]
floatList = []
doubleList :: [Double]
doubleList = [1, 1 + 1, 1 + 2]
列表的类型表达式通过在方括号中包裹另一种类型表达式来表示。由于列表的所有元素都必须是同一类型,方括号中的类型表达式就代表列表内部元素的类型。列表中的所有值(或能产生值的表达式)都必须属于这个类型。在上述例子中,即使是一个空列表(例如 floatList),也具有一个确定的类型。列表的类型告诉我们:该列表中元素的类型是什么,但它并不保证列表中一定存在元素。在 doubleList 的例子中,我们甚至可以看到列表中包含的是一些表达式(如 1 + 2),这些表达式在求值后会变成 Double 类型的值。这里我们还能看到 Haskell 的类型推导机制在起作用。doubleList 可以直接在 Haskell 程序中使用,编译器会自动推断出其中所有元素都是 Double 类型。但问题是:1 这个字面值也可能是 Int 类型呀?Haskell 为什么会知道它是 Double 呢?答案是:因为列表的类型被指定为 [Double]!Haskell 因此知道列表中的所有值都必须是 Double 类型。
列表是函数式编程语言的“主食”数据类型。例如 ML、Lisp(“list interpreter”的缩写)以及它们的衍生语言,都以列表作为核心数据结构之一。因此,学习 Haskell 中的列表,也能帮助你在许多其他语言(包括非函数式语言)中理解类似的概念。
另一种重要的数据类型是 元组。它与列表类似,都是一组值的序列,但有两个显著区别:
- 元组的长度是固定的。
- 元组中的元素可以有不同的类型。
元组的写法是:逗号分隔的值放在圆括号中。类型表达式的写法与值表达式类似,就像列表那样:
intPair :: (Int, Int)
intPair = (0, 1)
intFloatPair :: (Int, Float)
intFloatPair = (0, 1)
intCharDoubleTriple :: (Int, Char, Double)
intCharDoubleTriple = (1, 'a', 2)
septuple :: (Int, Float, Int, Float, Int, Float, Char)
septuple = (1, 1, 1, 1, 1, 1, 'a')
从这些例子中可以看到,我们可以将不同类型的值组合在一起形成复杂的类型。元组的长度可以任意(至少两个元素),而且不要求所有元素是同一类型。这种类型在需要将不同数据建立关联时非常有用,比如将一个整数与一个字符或浮点数配对存储。
2.2.3 函数类型(Function types)
现在我们来看最后一种(也许是最重要的)数据类型:函数。没错,函数本身就是一种数据类型!不仅如此,函数在 Haskell 中也是值(value)。到目前为止,我们主要编写的是一些基本的、主要是数值类型的表达式和值。但我们还没有真正解释,为什么之前定义的 square 实际上会变成一个可执行的函数。本质上,我们创建了一个值,并将它与名称 square 关联起来。
匿名函数(Anonymous functions)
首先,我们来看如何在不命名的情况下定义一个函数。这样的函数被称为 匿名函数(anonymous function)。在 Haskell 中,它们通过所谓的 lambda 抽象(lambda abstraction) 表示,形式如下:
\x -> x * x
这其实就是我们之前的平方函数。它接受一个参数 x,并产生表达式 x * x 的结果。我们也可以把这个函数值绑定到一个名字上:
square = \x -> x * x
这样,我们就得到了之前的 square 函数。它其实与我们原先的定义完全相同,只是写法不同而已。让我们看看这个值的类型:
square :: Int -> Int
square = \x -> x * x
可以看到,类型表达式的形式几乎与函数定义本身相似。就像函数把变量(例如 x)映射到某个表达式(如 x * x),类型表达式也说明了函数是如何将一个类型映射到另一个类型的。这里的意思是:square 接受一个 Int,返回另一个 Int。
这就是一个**一元函数(unary function)**的类型表达式——它只接受一个参数。
多参数函数(Curried function)
我们再看看如何定义一个二元函数(接受两个参数的函数):
add :: Int -> Int -> Int
add = \x -> \y -> x + y
在 Haskell 中,如果一个函数接收一个变量并返回一个表达式,那么这个表达式也可以是一个函数!我们可以通过在“内层”函数外加括号来更清晰地看到这一点:
add :: Int -> (Int -> Int)
add = \x -> (\y -> x + y)
不过这种写法显得既啰嗦又难读,所以 Haskell 提供了语法糖(syntactic sugar),让我们能更简洁地书写函数:
add :: Int -> Int -> Int
add = \x y -> x + y
我们看到,现在的 lambda 抽象一次性接受两个参数。甚至我们还可以再进一步简化——直接把参数写在函数名后面:
add :: Int -> Int -> Int
add x y = x + y
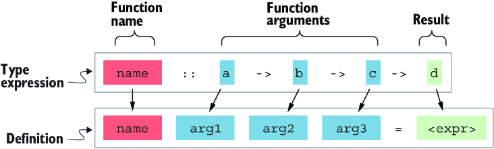
这就是我们在 Haskell 中最常用的函数定义方式。可以看出,lambda 抽象中的参数可以“移”到函数名后面。在许多其他语言中,函数的类型通常写作参数类型 + 返回类型的组合。Haskell 的函数类型表达式其实也可以这样理解:前面的类型代表参数类型,而最后一个类型代表函数**“返回值”的类型。这一点在 图 2.4 中有清楚的示意。不过这里的 “return” 一词被特意加上了引号。这是因为在函数式编程中,我们不应把函数理解为“返回”某个值——函数只是被求值(evaluated)为某个值**。
图 2.4:一个函数的类型表达式示例及其对应的定义
2.2.4 给数学运算加上类型(Adding types to math)
现在我们已经了解了类型是如何书写的,可以看到 Int -> Int 是 square 函数的一个合法类型。但为什么我们使用的是 Int 而不是其他数值类型呢?其实,没有特别的理由;然而,我们并不能随意更改类型。(*) 运算符可以作用于所有数值类型,但它要求两个参数的类型必须相同。如果我们给函数传入不同类型的值,就会遇到类型错误:
ghci> a = 1 :: Int -- #1
ghci> b = 2 :: Double -- #2
ghci> a * b
<interactive>:4:5: error:
• Couldn't match expected type 'Int' with actual type 'Double'
• In the second argument of '(*)', namely 'b'
In the expression: a * b
In an equation for 'it': it = a * b
- #1 指定变量
a的类型为Int - #2 指定变量
b的类型为Double
错误信息正如我们预期的那样:表达式 a * b 产生了类型错误,因为使用 a(类型为 Int)会强制 b 也必须是 Int 类型,而实际上 b 是 Double。
回想我们的加密算法,我们已经可以推测需要一个函数,它能将单个字符按指定的偏移量进行旋转,因此我们需要一个类型为 Int -> Char -> Char 的函数。不过,由于我们必须分别处理小写字母和大写字母,所以还需要考虑如何表示我们所使用的字符集和字母表。
2.3 关于字母表的一点帮助(A little help with the alphabet)
为了实现我们的算法,我们需要更深入地思考凯撒密码是如何工作的。正如图 2.5 所示,我们将每个字母替换为另一个字母,因此这种加密方法被称为替换密码。既然我们要实现这个密码,就必须问一个重要问题:我们如何处理字母和字母表?
图 2.5 凯撒密码概览
我们已经开始考虑我们要处理的数据类型。我们需要一个方法来指定偏移量,它可以是正数也可以是负数,因此 Int 类型可能就够用了。消息由一些字母组成,所以使用 String 类型可能比较合适。
2.3.1 为可读性定义同义类型(Synonymous types for readability)
等等,String?我们之前没见过这个类型。幸运的是,我们实际上已经隐式使用过它了。Haskell 中 String 的完整定义如下:
type String = [Char]
type 关键字定义了一个类型的简单同义词。因此,String 只是 [Char] 的别名。那么我们如何定义一个 String 值呢?
string1 :: String
string1 = "Hello World"
string2 :: String
string2 = ['H', 'e', 'l', 'l', 'o', ' ', 'W', 'o', 'r', 'l', 'd']
Haskell 和许多其他语言一样,为字符串提供了显式语法,这只是书写字符列表的一种更漂亮的方式。上述两个字符串是完全相同的。
现在我们知道要处理的类型,可以开始考虑实现算法所需的功能。无论最终方案如何,我们需要的函数都必须能够为单个字符生成替换字符。首先,我们需要一些工具函数来简化操作。在加密消息时,知道我们正在处理的字符类型非常有帮助。我们希望函数能够判断字符串中的字符是大写字母、小写字母、数字还是其他字符,其类型可以如下所示:
isUpper :: Char -> Bool
isLower :: Char -> Bool
isDigit :: Char -> Bool
isMisc :: Char -> Bool
实现这些函数需要我们判断一个 Char 是否属于某个字符集合。我们称这些集合为字母表。为此,我们首先定义一个字母表的类型同义词,本质上就是字符列表:
type Alphabet = [Char]
注意,字符串和字母表的类型完全相同,但类型的作用是表示该值的用途。String 用于显示在屏幕上,通常表示可读文本,而字母表类型意味着它表示我们要在替换密码中使用的字符集合,可以像图 2.1 所示那样旋转。
有了字母表类型后,我们可以开始定义字母表。例如,定义小写拉丁字母表:
lowerAlphabet :: Alphabet
lowerAlphabet = ['a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i', 'j',
'k', 'l', 'm', 'n', 'o', 'p', 'q', 'r', 's', 't',
'u', 'v', 'w', 'x', 'y', 'z']
不过,这样写比较繁琐。幸运的是,Haskell 支持范围语法(range):
ghci> [1 .. 10 :: Int]
[1,2,3,4,5,6,7,8,9,10]
ghci> [1, 5 .. 100 :: Int]
[1,5,9,13,17,21,25,29,33,37,41,45,49,53,57,61,65,69,73,77,81,85,89,93,97]
ghci> [0, -2 .. -10 :: Int]
[0,-2,-4,-6,-8,-10]
范围语法还支持步长,并且同样适用于 Char 类型。因此我们可以更简洁地定义字母表,如下所示(见清单 2.4):
清单 2.4 不同拉丁字母表和数字的定义
lowerAlphabet :: Alphabet
lowerAlphabet = ['a' .. 'z']
upperAlphabet :: Alphabet
upperAlphabet = ['A' .. 'Z']
digits :: Alphabet
digits = ['0' .. '9']
确保你的 GHCi 会话仍然打开,因为现在可以检查这些字母表!在 Lib.hs 中保存这些定义后,重新加载 GHCi:
ghci> :reload -- #1
[3 of 3] Compiling Lib ( .../src/Lib.hs, interpreted )
Ok, three modules loaded.
ghci> lowerAlphabet
"abcdefghijklmnopqrstuvwxyz"
ghci> upperAlphabet
"ABCDEFGHIJKLMNOPQRSTUVWXYZ"
ghci> digits
"0123456789"
- #1
:reload会重新加载模块,使模块中的新定义立即可用
如果之前关闭了 GHCi,会话也没关系,只需在 Lib.hs 保存字母表定义,然后在项目目录下再次执行 stack repl 即可。
⚠️ 警告:在 GHCi 中使用
:reload时,所有本地定义和变量都会被删除!该命令相当于关闭并重新打开 GHCi。
如你所见,字母表包含了我们需要的所有字符。但为什么它们被打印为 String?我们不是指定了自定义的字母表类型吗?在 GHCi 中使用 :type 命令检查:
ghci> :type lowerAlphabet
lowerAlphabet :: Alphabet
ghci> :type upperAlphabet
upperAlphabet :: Alphabet
ghci> :type digits
digits :: Alphabet
确实,它们是自定义类型。由于字母表是 Char 列表的同义词,并且几乎总是作为 String 使用,因此 Haskell 默认将其打印为 String。
使用类型同义词可以互换,但它的主要目的在于可读性:如果一个函数的参数类型是 Alphabet,我们就能推断出该函数会以特定方式处理这些字符。在这里,我们可以推断函数是为了加密算法而编写的。
FilePath 类型
标准库中也有类似的可读性用法。例如,FilePath 类型用于表示文件路径,但在 GHCi 中查看时会发现:
ghci> :info FilePath
type FilePath :: *
type FilePath = String
-- Defined in 'GHC.IO'
这个特殊类型本质上就是普通的 String(也就是 [Char]),但它可以提高函数的可读性:如果一个函数参数是 FilePath,就更清楚它期望的 String 格式是什么。
使用 :info 可以查看类型的定义和来源。
💡 提示:
:reload、:type和:info分别可以简写为:r、:t和:i。
2.3.2 字母的类型(The kinds of letters)
既然我们已经有了字母表,现在可以开始编写判断字符是否属于某个字母表的函数了。我们可以使用一个名为 elem 的函数。elem 是一个二元函数,需要两个参数:元素本身以及我们想要检查的列表。如果元素存在于列表中,它将返回 True,否则返回 False。由于我们的字母表类型 Alphabet 是 [Char] 的同义词,所以可以在字母表上使用这个函数。使用方法如下:
ghci> elem 'a' lowerAlphabet
True
ghci> elem 'a' upperAlphabet
False
ghci> elem '1' lowerAlphabet
False
ghci> elem '1' digits
True
Haskell 提供了一种语法小技巧来增强二元函数的可读性:
ghci> 'a' `elem` lowerAlphabet
True
任何二元函数都可以使用反引号写成中缀表示法!现在我们可以像读一句话一样理解代码:“a 是小写字母表中的元素吗?”
将这些函数组合起来,代码如下:
清单 2.5 检查字母表成员的辅助函数
isLower :: Char -> Bool
isLower char = char `elem` lowerAlphabet #1
isUpper :: Char -> Bool
isUpper char = char `elem` upperAlphabet #2
isDigit :: Char -> Bool
isDigit char = char `elem` digits #3
- #1 如果字符是小写字母则返回
True - #2 如果字符是大写字母则返回
True - #3 如果字符是数字则返回
True
在 GHCi 中测试这些函数:
ghci> :r
[3 of 3] Compiling Lib (.../src/Lib.hs, interpreted )
Ok, three modules loaded.
ghci> isLower 'a'
True
ghci> isLower 'A'
False
ghci> isUpper 'A'
True
ghci> isDigit '5'
True
2.3.3 逻辑组合(Logical combinations)
那如何判断一个字符是“杂项”(即不属于任何字母表)呢?可以使用布尔运算符:
isMisc :: Char -> Bool
isMisc char = not (isUpper char || isLower char || isDigit char)
布尔运算符有逻辑或 (||)、逻辑与 (&&) 和逻辑非 (not),它们的类型如下:
ghci> :type not
not :: Bool -> Bool
ghci> :type (||)
(||) :: Bool -> Bool -> Bool
ghci> :type (&&)
(&&) :: Bool -> Bool -> Bool
在 Haskell 中,运算符本质上是函数,使用括号可以将它们解释为函数,也可以写成前缀形式:
ghci> (||) False True
True
ghci> (+) 1 2
3
回到 isMisc 函数,虽然正确,但不易扩展。如果将来增加新的字母表,就必须写额外的辅助函数并添加到逻辑或中。更好的方法是检查字符是否不属于所有已有字母表。这时可以使用列表的追加运算符 (++):
ghci> [1,2,3] ++ [4,5,6]
[1,2,3,4,5,6]
ghci> "Hello" ++ " " ++ "World!"
"Hello World!"
注意,这个运算符同样适用于字符串,因为字符串本质上就是字符列表!此外,还有 notElem 函数,它是 elem 的否定形式。结合使用后,我们得到以下代码:
清单 2.6 判断字符是否既不是字母也不是数字的辅助函数
isMisc :: Char -> Bool
isMisc char = char `notElem` lowerAlphabet ++ upperAlphabet ++ digits #1
- #1 如果字符不属于小写字母、大写字母或数字,则返回
True
这样一来,扩展函数以支持更多字母表或其他不被视为杂项的字符,只需将新的字符列表追加到表达式中即可。
2.4 旋转转盘(Rotating the wheel)
现在我们已经有了辅助函数,可以开始考虑如何实现凯撒密码了。重点是理解如何在算法中进行简洁且恰当的大小写区分。
接下来需要完成的步骤:
- 获取字母在字母表中的索引。
- 获取字母表中某个索引对应的字母。
- 对字符串逐字符进行转换。
2.4.1 查找元素的索引(Finding an element’s index)
首先来看第一个子任务:查找列表中某个元素的索引。这需要两件事:首先遍历列表,其次跟踪索引。不过有一个小问题——Haskell 使用不可变数据。设置值后不能更改它。在 GHCi 中看起来似乎可以,但实际上不行。当你“更改”一个值时,实际上是在覆盖它。在函数中无法这样操作。此外,我们没有循环的概念。那么如何遍历列表呢?在纯函数式编程中,答案是递归。
函数可以基于自身定义,这就是递归的概念。因为无法使用循环,我们必须能够对数据的不同部分反复应用相同的定义。
让我们来看如何递归实现一个计算列表长度的函数。假设可以将列表分成第一个元素和剩余部分,那么列表长度可以定义为剩余部分的长度加一。剩余部分的长度则递归计算。但如何拆分数据结构呢?
这可以通过模式匹配实现。模式匹配是一个强大的语言特性,可以针对不同“模式”的数据编写函数定义。先看如何实现计算列表长度的函数。长度已知的列表是空列表:
listLength [] = 0
这里表示如果输入是空列表,结果就是 0。这个函数是部分函数,意味着存在未定义的输入。测试如下:
ghci> listLength []
0
ghci> listLength [1,2,3]
*** Exception: .../src/Lib.hs:...: Non-exhaustive patterns in function listLength
Haskell 告诉我们存在未匹配的输入,即模式不完整。如何让它完整呢?我们需要理解列表有两个构造子(constructors):[] 和 (:)。
[]:空列表(:):前置操作,将一个元素添加到现有列表前面
示例:
ghci> []
[]
ghci> 1 : []
[1]
ghci> 1 : [2,3]
[1,2,3]
ghci> 1 : 2 : 3 : []
[1,2,3]
这些构造子用于模式匹配。我们已经在定义中使用了 []。为了完整匹配,还需添加 (:) 构造子,这就是常见的列表模式匹配:
列表 2.7 列表模式匹配示例
listLength [] = 0 #1
listLength (x:xs) = ... #2
- #1 匹配空列表
- #2 匹配通过前置操作构建的列表
这可能看起来有些奇怪,但在 Haskell 中,你可以为不同的模式创建部分函数定义,本质上可以为每种模式定义完全不同的行为。
注:对于列表,我们介绍的这两种模式总是完整覆盖的!
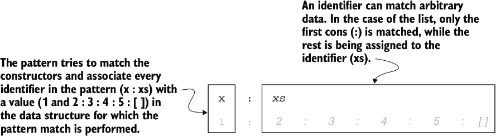
在 (x:xs) 模式中,x 表示列表的第一个元素(head),xs 表示剩余部分(tail)。如图 2.6 所示,如果列表只有一个元素,则 xs = []。列表长度计算方法:空列表长度为 0;非空列表长度为 1 + listLength xs,即第一个元素加上剩余部分的长度递归计算:
这里我们得到了第一个递归函数!如果列表有限,该函数会终止,因为最终会遇到 []。
图 2.6 非空列表的模式匹配
那么我们该如何计算列表的长度呢?显然,空列表的长度是 0,但如果列表由一个元素 x 和其余部分 xs 组成呢?正如我们之前讨论的那样,它的长度应当是 xs 的长度加 1,因为 x 是列表中的一个元素(必须被计数),而其余部分的长度是通过递归地计算 xs 的长度得到的。我们可以这样定义这个函数:
listLength [] = 0
listLength (x : xs) = 1 + listLength xs
这里我们得到了第一个递归函数!只要传入的列表是有限的,这个函数就会终止,因为定义最终会在遇到空列表 [] 时结束。
与计算列表长度的函数类似,获取某个元素在列表中的索引 也可以通过递归实现。当列表至少包含一个元素时,这个问题其实很简单: 如果第一个元素就是我们要找的那个,那么索引就是 0(因为索引从 0 开始);但如果不是,我们就要在当前列表的尾部继续查找。 我们可以这样开始定义:
indexOf :: Char -> [Char] -> Int
indexOf ch (x : xs) = if x == ch then 0 else 1 + indexOf ch xs
这个函数从列表开头开始检查。如果第一个元素就是目标元素,那么索引是 0;否则,我们在列表的尾部递归搜索。递归调用的结果会正好偏移 1(因为我们在递归时忽略了第一个元素),因此要将结果加 1。当然,这里假设递归调用的结果是正确的。现在关键的问题是:**当列表为空时怎么办?**此时没有正确的结果!因此,我们会显式地将这种情况定义为 undefined。完整的实现如下所示。
清单 2.8 在字符列表中计算字符索引的函数
indexOf :: Char -> [Char] -> Int
indexOf ch [] = undefined #1
indexOf ch (x:xs) = if x == ch then 0 else 1 + indexOf ch xs #2
- #1 当列表为空或递归结束时抛出异常
- #2 递归计算字符在列表中的索引
使用时必须确保字符存在于列表,否则程序会崩溃:
ghci> indexOf 'a' lowerAlphabet
0
ghci> indexOf 'f' lowerAlphabet
5
ghci> indexOf 'f' upperAlphabet
*** Exception: Prelude.undefined
注意:显式使用
undefined风格很差。我们将在第 3 章学习更好的处理方法。正确获取元素索引的函数是Data.List模块的elemIndex。
因为我们控制函数的使用,目前这样可以。但为了更明确地表示函数应在字母表上使用,而不是任意字符列表,可以修改类型:
indexOf :: Char -> Alphabet -> Int
2.4.2 查找给定索引处的元素
现在我们已经有了获取某个元素在列表中索引的方法,但我们还需要一个函数——可以根据索引取出列表中对应的元素。
幸运的是,Haskell 已经内置了这样的函数,叫做 (!!)。
它可以用中缀(infix)形式来调用,例如:
ghci> [1,2,3] !! 0
1
ghci> [1,2,3] !! 2
3
ghci> [1,2,3] !! 3
*** Exception: Prelude.!!: index too large
💡 练习:使用模式匹配编写 (!!) 函数
试着自己实现这个
!!函数,使用 模式匹配 和 递归 的方式。 如果索引过大或为负数,可以使用undefined让你的函数抛出异常。
与我们之前实现的 indexOf 类似,这个函数也存在某些输入没有有效结果的问题,因此使用时要非常小心!不过现在,我们可以编写真正的 字母轮盘旋转函数(参见图 2.1)。给定一个字符和一个整数偏移量,我们就能从字母表中取出正确的旋转结果:
upperRot :: Int -> Char -> Char
upperRot n ch = upperAlphabet !! ((indexOf ch upperAlphabet + n) `mod` 26)
lowerRot :: Int -> Char -> Char
lowerRot n ch = lowerAlphabet !! ((indexOf ch lowerAlphabet + n) `mod` 26)
我们通过将原字符的索引加上偏移量 n 来计算新的索引,并使用 mod 运算 实现轮盘循环(即超过末尾后重新从头开始)。由于英文字母表长度为 26,我们用 mod 26。例如:
ghci> upperRot 3 'Z'
'C'
ghci> upperRot (-3) 'C'
'Z'
然而,这两个函数本质上是重复的。我们可以将它们抽象成一个更通用的版本,让函数接受“字母表”作为参数。
📘 清单 2.9 通用字母表与大小写字母的旋转函数:
alphabetRot :: Alphabet -> Int -> Char -> Char
alphabetRot alphabet n ch =
alphabet !! ((indexOf ch alphabet + n) `mod` length alphabet)
upperRot :: Int -> Char -> Char
upperRot n ch = alphabetRot upperAlphabet n ch
lowerRot :: Int -> Char -> Char
lowerRot n ch = alphabetRot lowerAlphabet n ch
- #1 定义了针对任意字母表的通用旋转函数
- #2 定义大写字母的旋转函数
- #3 定义小写字母的旋转函数
这样,我们就得到了一个非常通用的旋转函数,可适用于任意字母表。
2.4.3 使用守卫控制流程(Guarding Control Flow)
现在,我们可以编写一个更通用的函数,用来根据输入字符自动选择合适的旋转规则。 我们的目标是:
- 对数字或空格等字符 不做变换;
- 对字母字符则使用前面定义的旋转函数。
最直接的方式是使用 if-then-else 语句:
ghci> x = 10 :: Int
ghci> if x > 5 then "x is larger than 5" else "x is not larger than 5"
"x is larger than 5"
不过在 Haskell 中,if 的语义和大多数语言不同——在 Haskell 里,if 必须有 else。因为它是一个表达式(不是语句),必须能返回一个值。一个没有 else 的 if 可能不会产生值,因此是非法的。我们可以写出这样的函数:
rotChar :: Int -> Char -> Char
rotChar n ch =
if isLower ch
then lowerRot n ch
else
if isUpper ch
then upperRot n ch
else ch
虽然这个函数是正确的,但可读性很差。嵌套的 if-then-else 不仅难以阅读,而且在分支很多的情况下非常笨拙。幸运的是,Haskell 提供了一个更优雅的方案——守卫(guards)。
在深入细节之前,让我们先看看使用 守卫(guards) 重写后的函数会是什么样子。如下所示:
📘清单 2.10 任意字符的旋转函数
rotChar :: Int -> Char -> Char
rotChar n ch
| isLower ch = lowerRot n ch -- #1
| isUpper ch = upperRot n ch -- #2
| otherwise = ch -- #3
- #1 检查参数是否为小写字母,若是则调用
lowerRot - #2 检查是否为大写字母,若是则调用
upperRot - #3 若不是字母(如空格或数字),则返回原字符
守卫(Guards)为我们提供了一种优雅的方式来指定条件(谓词)*及其对应的定义,就像模式匹配(pattern matching)一样!不过不同的是,这里我们匹配的不是模式,而是*布尔表达式。一般来说,任何布尔表达式都可以用作守卫条件。
注意 守卫和模式匹配都是按顺序执行的。如果某个模式或守卫先匹配成功,它就会优先被采用。这也是为什么那些“总是匹配成功”的情况应该放在最后。
那么,otherwise 是什么呢?有趣的是,它其实就是 True 的同义词!因为在大多数情况下,我们希望函数对所有输入值都有定义,所以最后一个守卫通常应该是 otherwise,它作为默认情况(catch-all)来兜底。
现在,让我们来测试一下我们的实现:
ghci> rotChar 13 'A'
'N'
ghci> rotChar 13 'a'
'n'
ghci> rotChar (-1) 'A'
'Z'
ghci> rotChar 10 '1'
'1'
ghci> rotChar 10 ' '
' '
2.5 转换字符串(Transforming a string)
现在我们已经能对单个字符进行旋转,接下来要解决的问题是:如何对一个字符串中的所有字符进行旋转?由于字符串(String)本质上就是字符列表([Char]),我们只需要将前面定义的 rotChar 函数应用到这个列表的每个元素即可。但是有一个问题:在 Haskell 中,所有数据都是不可变的,我们要如何“修改”列表呢?答案是:我们不能修改已有的值,而是要创建新的值!这是函数式编程的一个常见模式 —— 不修改旧数据,而是生成新的数据。我们可以利用之前学习的模式匹配,来编写一个实现凯撒密码(Caesar’s cipher)的函数:
caesar :: Int -> String -> String
caesar n [] = []
caesar n (x : xs) = rotChar n x : caesar n xs
空列表依然是空列表;而对于一个非空列表 (x : xs),我们将第一个元素 x 旋转后放在新列表的首位,然后递归地对剩余部分 xs 调用自身。例如:
ghci> caesar 13 "Caesars Cipher!"
"Pnrfnef Pvcure!"
ghci> caesar 13 (caesar 13 "Caesars Cipher!")
"Caesars Cipher!"
我们想要实现的目标,是把某种变换(这里是 rotChar)应用到整个列表上。这看起来是一个可以**推广(generalize)**的概念。
2.5.1 高阶映射(A higher-order mapping)
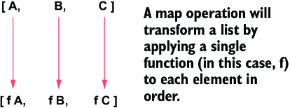
在函数式编程中,这种“对列表逐元素应用某种变换”的操作非常常见,因此值得进一步研究。我们可以把这种操作看作是一种映射(mapping):将列表中每个值映射到另一个值,但保持元素顺序不变。如图 2.7 所示,这是一个“从值到值”的转换关系。
图2.7 值的映射
如果我们想将 caesar 函数泛化为一个通用的 transform 函数,就需要把“函数本身”作为参数传入。请记住,函数在 Haskell 中也是一种值,因此我们完全可以把函数当作参数来使用!
观察 caesar 函数可以发现,参数 n 在通用情况下其实是不必要的,因为它只与 rotChar 有关。说到这里,我们需要用一个参数来替代 rotChar,我们将这个参数简单命名为 fun。这个参数代表一个可以“接收列表中单个元素并返回一个新的替代元素”的函数。由此,我们得到如下的函数定义:
transform fun [] = []
transform fun (x : xs) = fun x : transform fun xs
这个函数非常强大!来看几个例子:
ghci> transform (\x -> x + 1) [1..10] :: [Int]
[2,3,4,5,6,7,8,9,10,11]
ghci> transform (\x -> x > 5) [1..10] :: [Bool]
[False,False,False,False,False,True,True,True,True,True]
ghci> transform (\x -> if x == 'e' then 'u' else x) "Hello World!"
"Hullo World!"
当数据以列表形式存储时,这个函数能让我们轻松地对数据进行转换,而不需要手动拆分和重组列表。transform 代表了一类高阶函数(higher-order functions):它们不关心数据结构的内容,只关心如何对每个元素应用函数。任何接收函数作为参数的函数,都被称为高阶函数。它们是函数式编程的核心,因为它们能让我们抽象出通用算法并在不同场景下复用。
2.5.2 参数化类型(Parameterizing types)
这应该会让我们思考:如此通用的函数,它的类型会是什么样的呢?它的类型必须和定义一样通用。在 GHCi 中查看其类型,可以看到如下结果:
ghci> :type transform
transform :: (t -> a) -> [t] -> [a]
这些类型看起来有点奇怪:t?a?这里我们看到了 参数多态(parametric polymorphism) 的一个例子。也就是说,这个函数的类型并不是固定的,而是参数化的——我们可以用任意类型来替换 t 和 a。不过,当我们替换时,必须在所有出现该参数的地方替换为相同的类型。例如,当我们想用具体类型替换 t 时,就必须在整个类型表达式中把所有的 t 都替换掉。而 t 和 a 可以是不同的类型(当然,它们也可以是相同的)。
💡 注意 类型参数的名称其实无关紧要。
t也可以叫b,a也可以叫foo。
那么,这个类型表达式到底在告诉我们什么呢?它说明 transform 有两个参数:
- 第一个参数是一个函数,接收一个
t类型的值并返回一个a类型的值; - 第二个参数是一个
t类型值的列表([t]); - 整个函数返回一个
a类型值的列表([a])。
举个例子,假设我们有一个这样的函数:
f :: Int -> String
如果把它作为 transform 的第一个参数,那么:t 将被替换为 Int,a 将被替换为 String。这意味着第二个参数必须是 [Int],返回值则是 [String]:
ghci> :{
ghci| f :: Int -> String
ghci| f n = show n
ghci| :}
ghci> g xs = transform f xs
ghci> :t g
g :: [Int] -> [String]
这里我们也看到了 Haskell 的类型推导(type inference)在起作用——我们在脑中进行的替换,编译器同样可以自动完成!这种多态几乎存在于本书后续将遇到的每一个函数和数据类型中,因此熟悉它是非常重要的。它是编写抽象的、可组合的、通用代码的最基本概念之一。
💡 注意 参数多态类似于许多其他语言中的 泛型(generics) 概念, 例如 Java 或 Go。 在我们的例子中,类型变量就相当于“具有完全任意接口的泛型”。 在第 5 章,我们会学习如何在 类型类(type classes) 中对类型变量的性质进行约束。
高阶函数(higher-order functions)之所以有用,正是依赖于这种多态。我们不希望为不同的类型重复编写同样的函数,相反,我们希望找到最通用的类型,以便多次重用函数。transform 函数正是一个非常通用且重要的构建块,可以用来在列表上构建各种算法。
2.5.3 完整的凯撒密码(A finished cipher)
事实上,这个 transform 函数在 Haskell 中早已内置,它的名字就是——map。
map 接受两个参数:
- 一个函数(用于单个元素的变换)
- 一个列表(要处理的数据)
由于我们的加密函数需要对字符串中的每个字符进行字符轮换操作,我们完全可以使用 map 来实现 caesar 函数。
清单 2.11 实现凯撒密码(Caesar’s cipher)与 ROT13 的函数
caesar :: Int -> String -> String
caesar n message = map (\ch -> rotChar n ch) message -- #1
rot13 :: String -> String
rot13 message = caesar 13 message -- #2
#1使用字符旋转函数rotChar对消息中的每个字符进行变换;#2使用固定偏移量 13 的凯撒密码,实现 ROT13 编码。
到这里,我们终于得到了自己的加密函数(cipher)!当然,这个加密函数是通过我们在字符轮换中使用的偏移量参数化的。因此,ROT13 只是 凯撒密码(Caesar’s cipher) 的一个特例,非常容易由它构造出来。现在,我们也可以像古罗马人一样加密我们的通信了!
🧩 练习:ROT13.5 密码 (The ROT135 cipher)
ROT13 非常对称;不过,我们必须省略数字的轮换,因为如果连数字也轮换的话就会导致不对称——这是由于字母表与数字表的长度不同。然而,使用偏移量 5 进行数字的轮换可以让数字部分再次变得对称!你的任务是将 ROT13(字母) 与 ROT5(数字) 结合起来,形成一个ROT13.5,从而为拉丁字母与数字提供一个对称的编码方案!
编写一个函数 rot135,实现这种编码!
确保连续应用两次该函数会互相抵消:
ghci> rot135 "Hello 1 2 3 ... 7 8 9"
"Uryyb 6 7 8 ... 2 3 4"
ghci> rot135 (rot135 "Hello 1 2 3 ... 7 8 9")
"Hello 1 2 3 ... 7 8 9"
这样,我们就得到了一个**“绝对安全”的加密方案 😄。让我们回顾一下我们做了什么:我们首先创建了一个类型同义词 Alphabet,并定义了用于小写字母、大写字母和数字的常量,以明确表示我们处理的数据。接着,我们编写了函数来判断某个字符(Char)是否属于某个 Alphabet。基于这些定义,我们实现了一个在 Alphabet 中执行字符轮换的函数,并据此实现了凯撒密码(Caesar cipher)**。
🧮 练习:字符串频率分析(Frequency analysis)
ROT13 和凯撒密码并不是一种安全的“加密”方式。 这一点可以通过**频率分析(frequency analysis)**轻易证明。 在英语中,一些字母的出现频率远高于其他字母(例如,e 的出现频率远高于其他字母)。
请编写一个函数,用于计算某个字符在字符串中出现的次数:
count :: Char -> String -> Int
然后,使用这个函数对明文和“加密后的文本”执行频率分析。具体做法是:对我们之前定义的字母表中的每个字母应用该计数函数。思考:是否有办法编写一个基于频率分析的“最佳猜测”凯撒密码解密方案呢?
我们定义了一个自定义的类型同义词 Alphabet,以使代码更加清晰。通过字符区间(ranges),我们定义了小写字母表、大写字母表和数字表。在此基础上,我们实现了辅助函数,用于判断某个字符是否属于这些字母表之一。此外,我们还编写了函数,用于获取字符在字母表中的索引,以及在给定偏移量下执行字符轮换的函数。随后,我们将这些函数组合起来,构建了一个能够判断字符所属字母表并执行相应轮换的函数。最后,借助 map 函数,我们实现了**凯撒密码(Caesar cipher)**以及它的特例——ROT13 加密函数。
总结(Summary)
- 每个 Haskell 表达式都有一个类型表达式;为函数显式标注类型是良好实践。
- 使用
type关键字可定义类型同义词(type synonyms),让代码更具可读性。 - 在 GHCi 中使用
:type,:info,:reload(:t,:i,:r) 命令可查看类型、信息并重新加载模块。 - 任意二元函数都可以用反引号(```)写成中缀形式。
- **模式匹配(pattern matching)**可用于拆解数据结构,定义不同情况的函数。
- 定义递归函数时,我们假设递归调用的结果正确,以保证整体定义正确。
- **守卫(guards)**提供了基于布尔条件的简洁控制流,是 if-then-else 的优雅替代方案。
- map 函数用于依次对列表中每个元素应用函数。
- **参数多态(parametric polymorphism)**让我们能编写适用于任意类型的通用函数。
👉 我们在这一节中不仅实现了凯撒密码,还学习了高阶函数、类型多态与 map 的基本原理——这是理解函数式编程思想的核心。